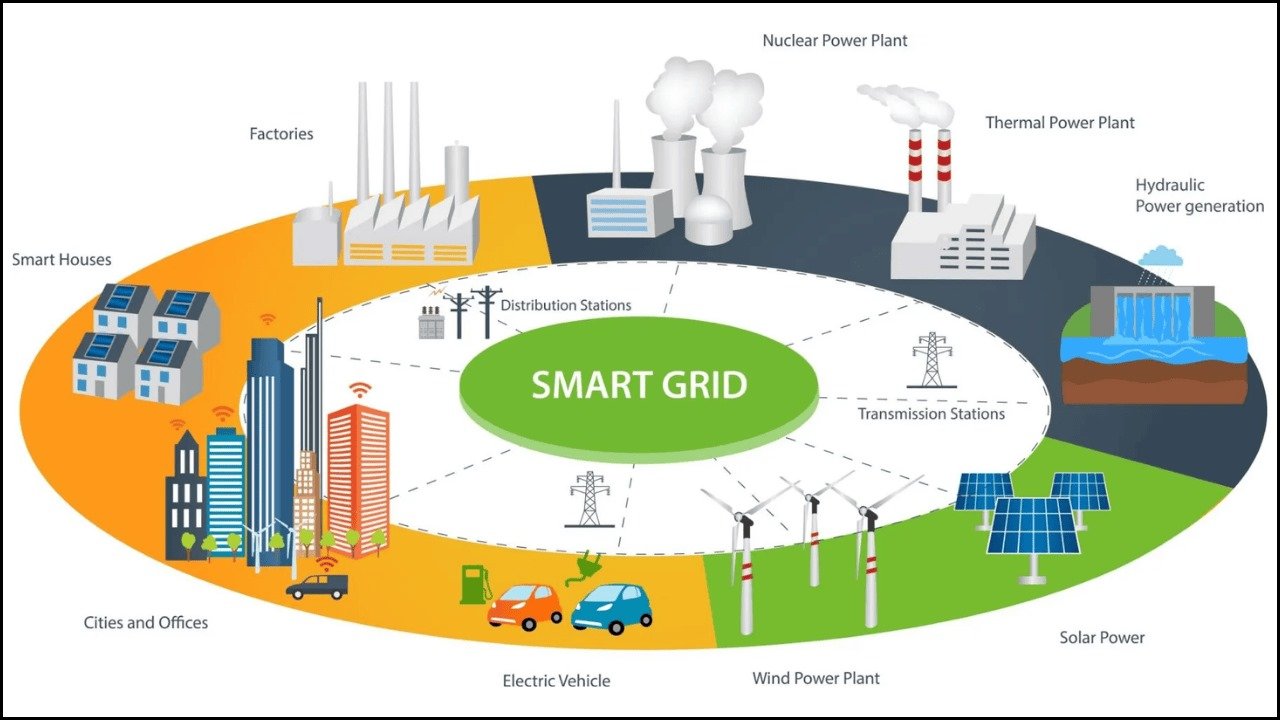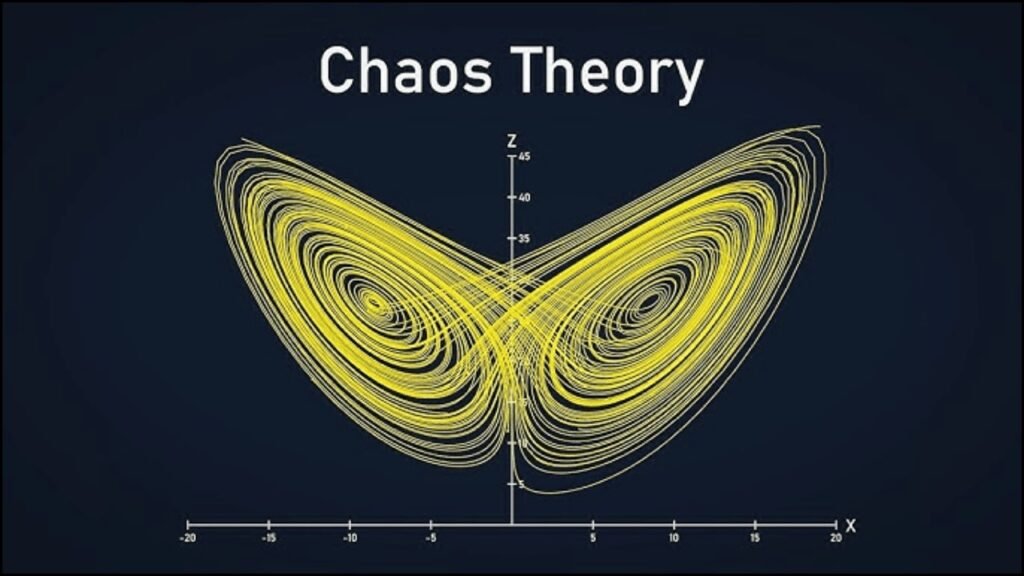
Chaos theory, a branch of mathematics and physics, studies systems that appear random but are governed by underlying deterministic rules. These systems are highly sensitive to initial conditions, meaning small changes can lead to vastly different outcomes, often referred to as the “butterfly effect.” Understanding chaos theory is essential for predicting and managing complex behaviors in real-world systems ranging from weather patterns to financial markets.
Table of Contents
Understanding Chaos Theory
Chaos theory focuses on non-linear dynamical systems, where outputs are not directly proportional to inputs. Unlike purely random systems, chaotic systems follow deterministic laws but exhibit unpredictable behavior due to sensitivity to initial conditions. Researchers use mathematical models, simulations, and fractal geometry to analyze and understand these patterns, providing insights into seemingly unpredictable phenomena.
Key Principles of Chaos Theory
- Sensitivity to Initial Conditions
Small differences in starting points can lead to vastly divergent outcomes, making long-term prediction challenging. - Nonlinearity
Chaotic systems exhibit non-linear relationships, meaning changes in input do not produce proportional changes in output. - Fractals and Self-Similarity
Many chaotic systems exhibit repeating patterns at different scales, known as fractals, which help in analyzing complex structures. - Deterministic Behavior
Despite unpredictability, chaotic systems follow underlying deterministic rules that can be modeled mathematically.
Applications of Chaos Theory in Real-World Systems
| Field | Application | Benefits |
|---|---|---|
| Meteorology | Weather prediction and climate modeling | Improved short-term forecasting and understanding of extreme events |
| Finance | Stock market analysis and risk assessment | Identifies patterns in market fluctuations and enhances decision-making |
| Engineering | Control systems and mechanical modeling | Helps design resilient systems and prevent failures |
| Biology | Population dynamics and ecosystem modeling | Predicts species interactions and ecosystem stability |
| Medicine | Heart rhythm and neurological modeling | Enhances diagnosis and treatment of arrhythmias and brain disorders |
1. Weather and Climate Systems
Weather systems are classic examples of chaotic behavior. Small variations in atmospheric conditions can lead to dramatically different weather outcomes. Chaos theory allows meteorologists to create models that improve the accuracy of short-term forecasts and provide probabilistic long-term climate projections.
2. Financial Markets
Stock prices and market indices exhibit chaotic patterns due to the interactions of numerous factors such as investor behavior, economic policies, and global events. Applying chaos theory enables analysts to detect hidden patterns, manage risks, and make informed investment decisions.
3. Biological Systems
From neural networks in the brain to population dynamics in ecosystems, many biological systems exhibit chaotic behavior. Understanding these patterns can aid in managing wildlife populations, predicting disease outbreaks, and modeling cardiac rhythms.
4. Engineering and Technology
Engineers apply chaos theory to optimize control systems, improve signal processing, and design robust mechanical systems. By analyzing system sensitivity, they can anticipate failures and enhance system resilience.
Challenges and Considerations
- Prediction Limitations: Long-term predictions remain difficult due to extreme sensitivity to initial conditions.
- Data Requirements: Accurate modeling requires precise and comprehensive data collection.
- Computational Complexity: Simulating chaotic systems often demands advanced computational resources.
- Interpretation: Translating mathematical models into actionable insights can be challenging in real-world scenarios.
Future Outlook
Chaos theory continues to expand its applications across science, engineering, and social sciences. Integration with machine learning and big data analytics is enhancing predictive modeling in chaotic systems. As computational power grows, researchers can simulate increasingly complex systems with greater accuracy, providing valuable insights into natural, technological, and economic phenomena.
FAQs
Q1: What is the main concept of chaos theory?
A1: It studies deterministic systems that are highly sensitive to initial conditions, leading to unpredictable outcomes.
Q2: How is chaos theory applied in weather forecasting?
A2: It models atmospheric dynamics, improving short-term forecasts and probabilistic long-term climate projections.
Q3: What are common challenges in applying chaos theory?
A3: Challenges include prediction limitations, data accuracy, computational demands, and interpreting complex models.